Maschinelles Lernen: Die 10 besten Algorithmen

Algorithmen des Maschinellen Lernens sind das Rückgrat intelligenter Systeme, da sie ihnen ermöglichen, Muster zu erkennen, Vorhersagen zu treffen und sich im Laufe der Zeit zu verbessern. In diesem Artikel werden die am häufigsten verwendeten Algorithmen untersucht.

1. Lineare Regression

Ein einfacher und weit verbreiteter Algorithmus zur Vorhersage kontinuierlicher Zielvariablen. Die lineare Regression (LR) ist eine grundlegende statistische Methode, die in der Datenwissenschaft und im maschinellen Lernen häufig zur Vorhersage einer kontinuierlichen Zielvariablen auf der Grundlage einer oder mehrerer Eingabefeatures verwendet wird. Ihre Einfachheit und Interpretierbarkeit machen sie sowohl bei Anfängern als auch bei erfahrenen Anwendern zu einer beliebten Wahl.

Was ist Lineare Regression?

Die lineare Regression versucht, die Beziehung zwischen einer abhängigen Variable (Ziel) und einer oder mehreren unabhängigen Variablen (Features) darzustellen, indem sie eine lineare Gleichung an die beobachteten Daten anpasst. Die allgemeine Form lautet:

\( y =w_0 + w_1∙ x_1 + w_2∙ x_2 +…+ w_n∙ x_n + ε \)

wobei:

y die abhängige Variable ist.
\( x_1, x_2, x_n \) die unabhängigen Variablen sind.
\( w_0 \) den Achsenabschnitt darstellt.
\( w_1, w_2, w_n \) die Koeffizienten sind.
\( ε \) der Fehlerterm ist.

Arten der Linearen Regression:

Einfache Lineare Regression (Simple LR): Beinhaltet eine einzige unabhängige Variable. Die Beziehung wird als gerade Linie modelliert:
\( y = w_0 + w_1∙ x_1 + ε \)
Mehrfache Lineare Regression (Multiple LR):
\( y = w_0 + w_1∙ x_1 + w_2∙ x_2 +…+ w_n∙ x_n + ε \)

An jedem Punkt gibt es zwei Werte – den tatsächlichen und den vorhergesagten Wert des Modells. Die lineare Regression berechnet die quadrierten Abweichungen zwischen ihnen. Dies wird durch eine Methode namens „Kleinste-Quadrate-Schätzung“ (Ordinary Least Squares, OLS) erreicht.

2. Logistische Regression

Die logistische Regression ist eine grundlegende statistische Methode, die für binäre Klassifikationsaufgaben verwendet wird. Sie sagt die Wahrscheinlichkeit eines binären Ergebnisses voraus, das entweder 0 oder 1, wahr oder falsch sein kann. Diese Technik wird aufgrund ihrer Einfachheit und Effektivität in verschiedenen Bereichen wie Medizin, Finanzen und Sozialwissenschaften häufig eingesetzt.

Verständnis der Logistischen Regression

Im Gegensatz zur linearen Regression, die ein kontinuierliches Ergebnis vorhersagt, wird die logistische Regression verwendet, wenn die abhängige Variable kategorisch ist. Die logistische Funktion oder Sigmoid-Funktion ist grundlegend für die logistische Regression. Sie ordnet jeder reellen Zahl einen Wert zwischen 0 und 1 zu, was sie für die Wahrscheinlichkeitsabschätzung geeignet macht.

Die logistische Funktion wird definiert als:

sigma(z) = 1/(1 + e^(-z))

wobei (z) die lineare Kombination der Eingabefeatures ist.

Das Training eines logistischen Regressionsmodells beinhaltet das Finden der bestpassenden Parameter (Gewichte), die die Differenz zwischen den vorhergesagten Wahrscheinlichkeiten und den tatsächlichen binären Ergebnissen minimieren. Dies wird in der Regel durch eine Technik namens „Maximum-Likelihood-Schätzung“ (MLE) erreicht. Die logistische Regression bleibt ein leistungsstarkes und weit verbreitetes Werkzeug für binäre Klassifikationsaufgaben. Ihre Fähigkeit, Wahrscheinlichkeitsabschätzungen zu liefern, macht sie besonders wertvoll in Bereichen, in denen Entscheidungsfindung auf Risikobewertung und Prognose basiert.

3. Support Vector Machine (SVM)

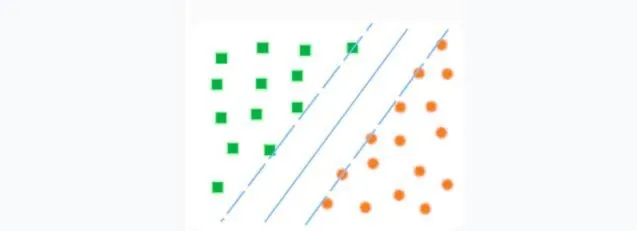
Was ist eine Support Vector Machine? Diese Methode ist mit binären Klassifikatoren (wenn es nur zwei Klassen gibt) verbunden. Die Grundidee von SVM ist einfach: Es wird untersucht, wie man zwei Linien zwischen den Kategorien ziehen kann, um den größtmöglichen Abstand zu schaffen.

Support Vector Machine (SVM)

Quelle: Skillbox

In wissenschaftlicheren Begriffen kann man sagen: Eine Support Vector Machine (SVM) ist ein Algorithmus des maschinellen Lernens, der sowohl für Klassifikation als auch für Regression verwendet wird. Sie basiert auf der Idee, dass Datenpunkte in zwei Gruppen unterteilt werden können, indem ein Hyperplane durch diese Punkte gezogen wird.

Um diesen Hyperplane zu erstellen, verwendet die Support Vector Machine sogenannte Support-Vektoren. Dies sind Datenpunkte, die an der Grenze zwischen den Gruppen liegen. Diese Support-Vektoren bestimmen die Richtung und den Abstand vom Hyperplane zu jedem Datenpunkt.

Auf diese Weise ermöglicht es die Support Vector Machine, festzustellen, zu welcher Gruppe die Datenpunkte gehören, und diese Daten zu nutzen, um ein Modell zu erstellen, das zur Vorhersage neuer Daten verwendet werden kann.

Was man über SVM wissen muss:

Mathematische Grundlagen der Support Vector Machines: SVM basiert auf einem linearen Modell, das einen Hyperplane definiert, der die Daten in zwei Kategorien trennt.

Wahl einer Kernel-Funktion: Die Wahl der Kernel-Funktion ist ein entscheidender Faktor bei der Verwendung von SVM. Die Kernel-Funktion ermöglicht es der SVM, mit nichtlinearen Funktionen zu arbeiten, was ihre Leistung bei einigen Problemen verbessern kann.

Optimierung der Hyperparameter: SVM hat mehrere Hyperparameter, die angepasst werden müssen, um die besten Ergebnisse zu erzielen. Zu diesen Parametern gehören der Regularisierungskoeffizient, die Fehlerstrafe, die Kernel-Funktion usw.

Modellanpassung: Nach der Anpassung der Hyperparameter muss das Modell auf den Trainingsdaten angepasst werden. Dies beinhaltet die Berechnung der Hyperplan-Koeffizienten und die Optimierung der Zielfunktion.

Bewertung der Modellqualität: Nach der Anpassung des Modells muss seine Qualität anhand der Testdaten bewertet werden.

4. Entscheidungsbaum

Ein Entscheidungsbaum funktioniert, indem er die Daten basierend auf den Merkmalswerten in Äste aufteilt, was ihn leicht verständlich und visualisierbar macht. Entscheidungsbäume werden aufgrund ihrer Einfachheit und Effektivität in verschiedenen Bereichen wie Finanzen, Gesundheitswesen und Marketing häufig eingesetzt.

Ein Entscheidungsbaum besteht aus Knoten und Ästen. Jeder interne Knoten repräsentiert eine Entscheidung basierend auf einem Merkmal, jeder Ast stellt das Ergebnis dieser Entscheidung dar, und jedes Blatt (Leaf-Node) repräsentiert eine endgültige Vorhersage oder ein Ergebnis. Der Prozess des Aufbaus eines Entscheidungsbaums beinhaltet die Auswahl des besten Merkmals zur Aufteilung der Daten an jedem Knoten, was typischerweise mit Kriterien wie Gini-Impurity oder Informationsgewinn geschieht.

Wichtige Konzepte:

Wurzelknoten (Root Node): Der oberste Knoten eines Entscheidungsbaums, der das gesamte Datenset repräsentiert.
Interne Knoten (Internal Nodes): Knoten, die Entscheidungen basierend auf Merkmalswerten darstellen.
Blattknoten (Leaf Nodes): Endknoten, die die endgültige Vorhersage oder das Ergebnis darstellen.
Aufteilung (Splitting): Der Prozess, bei dem ein Knoten basierend auf einem Merkmal in zwei oder mehr Unterknoten aufgeteilt wird.
Beschneiden (Pruning): Der Prozess, Teile des Baums zu entfernen, um Überanpassung zu verhindern und die Generalisierung zu verbessern.

Verfahren zum Aufbau eines Entscheidungsbaums:

Auswahl des besten Merkmals: Wählen Sie das Merkmal, das die Daten am besten aufteilt, basierend auf einem gewählten Kriterium (z. B. Gini-Impurity, Informationsgewinn).
Aufteilung der Daten: Teilen Sie das Datenset basierend auf dem ausgewählten Merkmal in Teilmengen auf.
Wiederholen: Wenden Sie den Prozess rekursiv auf jede Teilmenge an, bis eine Abbruchbedingung erfüllt ist (z. B. maximale Tiefe, minimale Anzahl von Stichproben pro Blatt).

5. Random Forest

Dieser Ansatz nutzt kollektive Intelligenz, indem er die Vorhersagen mehrerer Entscheidungsbäume kombiniert, was zu einem präziseren und zuverlässigeren Modell führt. Random Forest besteht aus zahlreichen einzelnen Entscheidungsbäumen, die zusammen als Ensemble fungieren. Jeder Baum im Wald wird aus einer zufälligen Teilmenge der Trainingsdaten und einer zufälligen Teilmenge von Merkmalen aufgebaut. Die endgültige Vorhersage erfolgt durch Mittelung der Vorhersagen aller Bäume (für Regression) oder durch Mehrheitswahl (für Klassifikation).

Wichtige Konzepte:

Bootstrap Aggregation (Bagging): Random Forest verwendet Bagging, um mehrere Teilmengen des ursprünglichen Datensatzes durch Stichproben mit Zurücklegen zu erstellen. Jede Teilmenge wird verwendet, um einen anderen Entscheidungsbaum zu trainieren.
Zufällige Merkmalsauswahl: Bei jeder Aufteilung im Entscheidungsbaum wird eine zufällige Teilmenge von Merkmalen in Betracht gezogen, was hilft, die Korrelation zwischen den Bäumen zu verringern und die Modelldiversität zu erhöhen.
Ensemble-Vorhersage: Die Vorhersagen aller Bäume werden kombiniert, um die endgültige Ausgabe zu erzeugen, was hilft, die Varianz zu reduzieren und die Genauigkeit zu verbessern.

Der Prozess des Aufbaus eines Random Forest:

Erstellung von Bootstrapped-Datensätzen: Erstellen Sie mehrere Teilmengen der Trainingsdaten durch Stichproben mit Zurücklegen.
Training der Entscheidungsbäume: Bauen Sie für jede Teilmenge einen Entscheidungsbaum unter Verwendung einer zufälligen Teilmenge von Merkmalen bei jeder Aufteilung.
Aggregieren der Vorhersagen: Kombinieren Sie die Vorhersagen aller Bäume, um die endgültige Vorhersage zu treffen.

6. Naive Bayes-Klassifikator

Dieser Algorithmus ist besonders effektiv für Textklassifizierungsaufgaben wie Spam-Erkennung, Sentiment-Analyse und Dokumentenkategorisierung. Trotz seiner Einfachheit liefert Naive Bayes oft überraschend gute Ergebnisse und ist eine beliebte Wahl für viele reale Anwendungen. Naive Bayes-Klassifikatoren gehen davon aus, dass die Merkmale unter der Bedingung des Klassenlabels bedingt unabhängig sind, was eine starke Annahme ist und in der Praxis oft nicht zutrifft. Diese „naive“ Annahme vereinfacht jedoch die Berechnungen und funktioniert in vielen Szenarien gut.

Naive Bayes wird ausgedrückt als:

\( P(C|X) = (P(X|C) ∙ P(C)) / P(X) \)

Wo:

• P(C|X) ist die a-posteriori Wahrscheinlichkeit der Klasse ( C ) gegeben die Merkmale ( X ).
• P(X|C) ist die Wahrscheinlichkeit der Merkmale ( X ) gegeben die Klasse ( C ).
• P(C) ist die Wahrscheinlichkeit der Klasse ( C ).
• P(X) ist die Wahrscheinlichkeit der Merkmale ( X ).

Arten von Naive Bayes-Klassifikatoren:

Multinomiales Naive Bayes: Geeignet für diskrete Daten, häufig verwendet für Textklassifizierungen, bei denen Merkmale Wortfrequenzen darstellen.
Bernoulli Naive Bayes: Verwendet für binäre/boole’sche Merkmale, wie z. B. das Vorhandensein oder Fehlen eines Wortes in einem Dokument.
Gaussian Naive Bayes: Geht davon aus, dass die Merkmale einer Normalverteilung folgen, verwendet für kontinuierliche Daten.

Der Naive Bayes-Klassifikator ist ein robustes und effizientes Werkzeug für Textklassifizierungsaufgaben. Seine probabilistische Natur und Einfachheit machen ihn zu einem wertvollen Bestandteil des Machine-Learning-Toolkits, insbesondere für Anwendungen mit großen Datensätzen und hochdimensionalen Merkmalsräumen.

7. K-Nearest Neighbors (KNN)

K-Nearest Neighbors (KNN) ist ein nicht-parametrischer, instanzbasierter Lernalgorithmus, der für Klassifizierungs- und Regressionsaufgaben verwendet wird. Er kategorisiert Datenpunkte, indem er die vorherrschende Klasse unter ihren nächsten Nachbarn im Merkmalsraum identifiziert. Trotz seiner Einfachheit ist KNN äußerst effektiv und wird in verschiedenen Anwendungen eingesetzt, darunter Mustererkennung, Data Mining und Intrusionserkennung.

Funktionsweise von KNN:

KNN basiert auf dem Prinzip, dass ähnliche Datenpunkte im Merkmalsraum nahe beieinander liegen. Der Algorithmus bestimmt die Klasse eines neuen Datenpunkts, indem er die ‚k‘ nächsten Nachbarn untersucht und ihm die am häufigsten vorkommende Klasse zuweist. Der Wert von ‚k‘ ist ein entscheidender Parameter, der bestimmt, wie viele Nachbarn berücksichtigt werden.

Algorithmus-Schritte:

Wählen Sie die Anzahl der Nachbarn (k): Wählen Sie die Anzahl der zu berücksichtigenden nächsten Nachbarn aus.
Berechnen Sie die Entfernung: Berechnen Sie die Entfernung (Manhattan, Euklidisch, Minkowski) zwischen dem neuen Datenpunkt und allen anderen Punkten im Datensatz.
Identifizieren Sie die nächsten Nachbarn: Wählen Sie die ‚k‘ Datenpunkte mit den geringsten Entfernungen zum neuen Punkt aus.
Klassifizieren: Weisen Sie die Klasse zu, die unter den ‚k‘ nächsten Nachbarn am häufigsten vorkommt.

8. K-Means-Clustering

K-Means-Clustering ist ein beliebter Algorithmus des unüberwachten Lernens, der verwendet wird, um Daten basierend auf der Ähnlichkeit von Merkmalen in (k) Cluster zu unterteilen. Er wird in verschiedenen Bereichen wie Marktsegmentierung, Bildkompression und Mustererkennung weit eingesetzt. Der Algorithmus zielt darauf ab, die Varianz innerhalb jedes Clusters zu minimieren, was ihn zu einem leistungsstarken Werkzeug zur Entdeckung zugrunde liegender Muster in Daten macht.

Der K-Means-Algorithmus funktioniert, indem er Datenpunkte iterativ Clustern zuweist und die Clusterzentren aktualisiert, bis eine Konvergenz erreicht ist. Das Ziel ist es, die Daten in (k) Cluster zu partitionieren, wobei jeder Datenpunkt dem Cluster mit dem nächstgelegenen Mittelwert (Zentrum) zugeordnet wird.

Algorithmus-Schritte:

Zentren initialisieren: Wählen Sie zufällig (k) Datenpunkte als anfängliche Clusterzentren aus.
Cluster zuweisen: Weisen Sie jeden Datenpunkt dem nächstgelegenen Zentrum basierend auf einer Distanzmetrik (häufig euklidische Distanz) zu.
Zentren aktualisieren: Berechnen Sie die neuen Zentren, indem Sie den Mittelwert aller Datenpunkte, die jedem Cluster zugeordnet sind, ermitteln.
Wiederholen: Wiederholen Sie die Zuweisungs- und Aktualisierungsschritte, bis sich die Zentren nicht mehr signifikant ändern oder eine maximale Anzahl an Iterationen erreicht ist.

K-Means Clustering Algorithmus Schritte

Quelle: Medium: Christos Panourgias

Die Einfachheit und Effizienz des K-Means-Clustering machen ihn zu einer beliebten Wahl für verschiedene Anwendungen, von der Marktsegmentierung bis zur Bildkompression. Es ist jedoch wichtig, die Anzahl der Cluster und die Methoden zur Initialisierung sorgfältig zu berücksichtigen, um optimale Ergebnisse zu erzielen.

9. Clustering mit DBSCAN

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) ist ein leistungsstarker Algorithmus des unüberwachten Lernens, der für Clustering-Aufgaben verwendet wird. Im Gegensatz zu traditionellen Clustering-Methoden wie K-Means kann DBSCAN Cluster beliebiger Form identifizieren und ist besonders effektiv im Umgang mit Rauschen und Ausreißern. Er wird häufig in Bereichen wie geospatialer Analyse, Bildverarbeitung und Anomalieerkennung eingesetzt.

DBSCAN gruppiert Punkte, die eng beieinander liegen, und kennzeichnet Punkte, die weit entfernt sind, als Ausreißer. Der Algorithmus basiert auf zwei Schlüsselparametern: epsilon (ε), der den Radius einer Nachbarschaft um einen Punkt definiert, und minPts, der die minimale Anzahl an Punkten angibt, die erforderlich ist, um eine dichte Region (Cluster) zu bilden.

Algorithmus-Schritte:

Punkt auswählen: Beginnen Sie mit einem beliebigen Punkt im Datensatz.
Nachbarschaftsprüfung: Finden Sie alle Punkte innerhalb des ε-Radius des ausgewählten Punktes.
Identifikation des Kernpunkts: Wenn die Anzahl der Punkte in der Nachbarschaft größer oder gleich minPts ist, markieren Sie den Punkt als Kernpunkt und bilden Sie ein Cluster.
Cluster erweitern: Fügen Sie rekursiv alle dichte-erreichbaren Punkte (Punkte innerhalb der ε-Distanz zu einem Punkt im Cluster) zum Cluster hinzu.
Wiederholen: Setzen Sie den Prozess für alle Punkte im Datensatz fort.

Clustering mit dem DBSCAN-Algorithmus:

Quelle: Medium: Christos Panourgias

10. Hauptkomponentenanalyse (PCA)

Die Hauptkomponentenanalyse (PCA) ist eine beliebte Methode in der Statistik zur Reduzierung der Dimensionen in einem Datensatz. Sie reduziert hochdimensionale Daten auf ein niedriger dimensionales Format und bewahrt dabei so viel Variabilität wie möglich. PCA ist besonders nützlich in Bereichen wie Datenvisualisierung, Bildverarbeitung und explorativer Datenanalyse, wo die Reduzierung der Variablen die Modelle vereinfachen und wichtige Muster hervorheben kann.

Verstehen von PCA:

PCA funktioniert, indem es die Richtungen (Hauptkomponenten) findet, die die Varianz innerhalb der Daten maximieren. Diese Hauptkomponenten sind orthogonal zueinander, was sicherstellt, dass sie unterschiedliche Muster in den Daten erfassen. Die erste Hauptkomponente erklärt die meiste Varianz, die zweite erfasst die nächsthöhere Menge, und so weiter.

Algorithmus-Schritte:

Daten standardisieren: Stellen Sie sicher, dass jede Eigenschaft einen Mittelwert von null und eine Standardabweichung von eins hat.
Kovarianzmatrix berechnen: Berechnen Sie die Kovarianzmatrix, um zu verstehen, wie die Eigenschaften in Bezug aufeinander variieren.
Eigenwerte und Eigenvektoren berechnen: Bestimmen Sie die Eigenwerte und Eigenvektoren der Kovarianzmatrix. Die Eigenvektoren repräsentieren die Hauptkomponenten, und die Eigenwerte geben an, wie viel Varianz von jeder Komponente erfasst wird.
Hauptkomponenten sortieren und auswählen: Sortieren Sie die Eigenwerte in absteigender Reihenfolge und wählen Sie die obersten (k) Eigenvektoren aus, die den größten Eigenwerten entsprechen.
Daten transformieren: Projizieren Sie die ursprünglichen Daten auf die ausgewählten Hauptkomponenten, um die reduzierte Dimension darzustellen.

Durch die Transformation hochdimensionaler Daten in eine nieder-dimensionalere Form hilft PCA, wichtige Muster aufzudecken und komplexe Datensätze zu vereinfachen.

Fazit

In diesem Artikel haben wir einige der am häufigsten verwendeten Algorithmen des maschinellen Lernens untersucht, von denen jeder seine eigenen Stärken und Anwendungen hat. Diese Algorithmen bilden die Grundlage intelligenter Systeme, die es ihnen ermöglichen, Muster zu erkennen, Vorhersagen zu treffen und sich im Laufe der Zeit zu verbessern. Jeder Algorithmus hat seine einzigartigen Vorteile und Einschränkungen, was sie für verschiedene Arten von Problemen und Datensätzen geeignet macht. Durch das Verständnis und die Anwendung dieser Algorithmen können wir effektivere und effizientere Modelle des maschinellen Lernens entwickeln.